2024-11-25总结

游戏人生

考虑到当 \(k=3\) 时，跑得最慢。

考虑怎么优化，因为当你处理到 \(B=N^{\frac{1}{k+1}}\) 的质数时，后面只可能是 \(k\) 个数相乘，所以我们处理到这里之后直接判断能不能刚好开 \(k\) 次根就好了。

例如当 \(k=3\) 时直接处理到 \(32771\) 的质数之后直接判断能不能开三次根就好了。

注意，开根用 qpow(x,1.0/k) 时不要忘了 1.0。

逆序对

我们只会操作 \((x,y)\) 当 \(a_x\ge a_y\)。

发现操作的左端点只能是前缀最大值，否则扩大之后不会变劣，右端点也只能是后缀最大值。

正难则反，考虑一个数怎么产生贡献：

当 \(x<y<z\) 时，对于 \(a_x>a_y>a_z\)，\(y\) 对于操作 \((x,z)\) 区间会产生 \(2\) 的贡献。

直接扫描线维护即可。

如果有相同的数（这题没有，但 バブルソート (Bubble Sort) - 洛谷 | 计算机科学教育新生态 这个有），那么当 \(a_y=a_x\) 时 或 \(a_y=a_z\) 时只会产生 \(1\) 的贡献，如果都相等，就只会产生 \(0\) 的贡献。

那么我们只需要建两个矩形，一个是左端点包括相等右端点不包括，\(1\) 的贡献，一个是左端点不包括右端点包括，\(1\) 的贡献，那么如果都不相等刚好为 \(2\) 的贡献，之和一个相等刚好为 \(1\) 的贡献。都相等刚好为 \(0\) 的贡献。

图论考试

大家都用了克鲁斯卡尔，但我用了 Prim。

就是考虑模拟 Prim 的过程，然后她不是每次将距离点集最近的点找出来吗，就是用线段树维护 dis，每次操作就是找出最小的数 x，然后将每个数更新为 \(\min(a_i,a_x)\)，注意这里可能有一些和 \(x\) 连过边的不能被更新，可以直接先在更新前暴力询问她们的值，然后更新完后再暴力还原回去就可以了。

然后我们需要将 \(x\) 的值赋值为 \(\infty\)。

步行

听说是很经典的结论，但是我不会/wul。

先考虑答案怎么计算： \[ \sum d_i+d_{i+1}-d_{lca} \] 然后前面的因为 \(v_i\) 都相等，所以贡献是一样的，那么我们是不是要让她的 \(d_{lca}\) 尽可能小。

当 \(lca\) 为根时，她最小。

那什么时候 lca 为根，当 \(i\) 和 \(i+1\) 不在一个子树内时！

当 \(lca\) 为（带权）重心时，它的每一个子树大小都小于等于 \(sum/2\)，那么就可以满足上述条件！

考虑添加修改，我们先钦定 \(a\) 是 \(b\) 的 fa，\(c\) 是 \(b\) 的孙子，\(d\) 不是 \(b\) 的孙子：

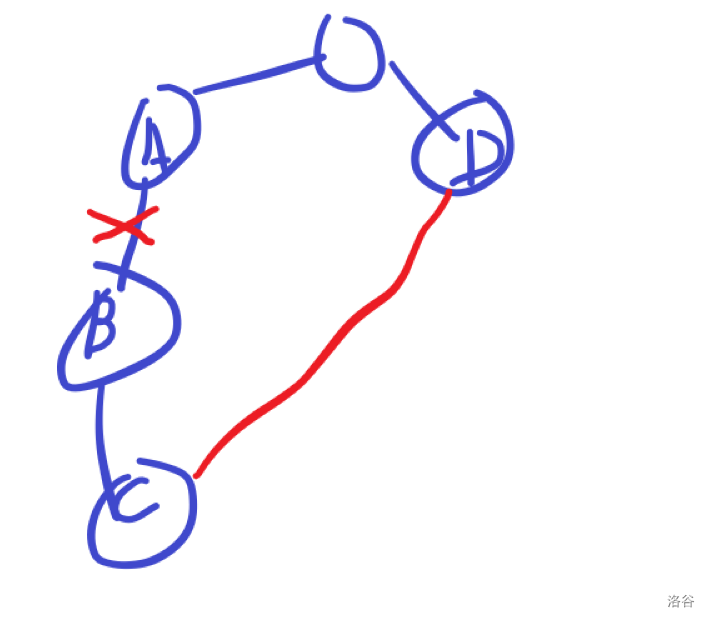
如果 \(D\) 和 \(C\) 的lca不是原本的重心 \(rt\) 时，显然它们即使断边连边后也在一个子树内，重心不变。

否则我们新的重心一定在原本的重心到 \(D\) 的链上，直接从 \(D\) 倍增网上跳求重心，也就是要求 \(sz_u+sz_B<=sum/2\)。

考虑求完重心怎么求每个点到她的距离。

显然先可以用换根求出没有修改前每个点到她的距离。

修改后只有 \(B\) 子树内的距离会改变。

先把错误的距离删去，也就是删除 \(B\) 子树内到 \(u\) 的距离（没有修改的）

然后添加正确的距离，也就是添加 \(B\) 子树内到 \(u\) 的距离（修改后的）

注意到前面这个很好求，但后面这个我们遇到了挫折。

可以用容斥，先求出每个点到 \(C\) 的距离（没有修改的），然后删去B外面到C的距离（没有修改的），就可以得到B内到达C 的距离。

前面都是好求的，所以都很好求。

然后做完了，\(O(n\log n)\)。