【施工】多面体中的欧拉公式的感性理解

1750 年，欧拉在给他的好友哥德巴赫的信中提到，他发现了一个事实：

任何凸多面体的面的个数（\(F\)），减去边的个数（\(E\)），再加上顶点的个数（\(V\)），等于 \(2\)。

这个发现被写为： \[ F-E+V=2 \] 例如一个立方体，有 \(6\) 个面，\(12\) 条边，\(8\) 个顶点，\(6-12+8\) 正好等于 \(2\)。

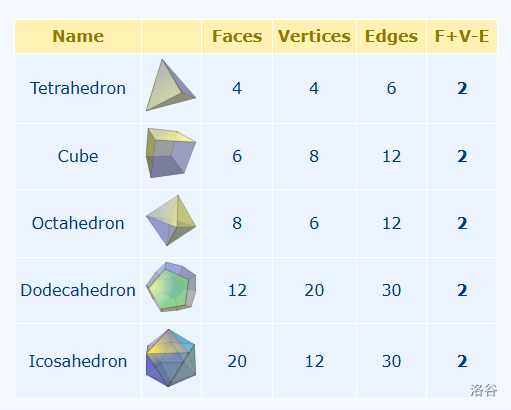
考虑证明这一个结论。

首先，立面图肯定不如平面图。

所以考虑将凸多面体投射到平面上，如下图所示：

观察新生成的平面图形，它的点数不变，边数也不变，但是面数减少了一个。（必定存在恰好一个面被遮住无法投射出来）

这个结论的证明较为繁琐，而且由于笔者能力有限，这里不给出证明。

那么我们只需要证明这个投射后的平面图满足 \(F-E+V=1\)，就可以证明原先的凸多面体满足 \(F-E+V=2\)。

观察投射后的平面图，它是由若干个多边形组成的。而每一个多边形都可以分解为一些三角形的组合，所以整个投射后的平面图可以分解为三角形的组合，如：

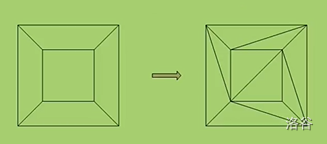
而每次添加一条分割线，都会使得 \(F\) 加一，\(E\) 加一，所以 \(F-E+V\) 的值不变。

我们通过归纳法，逐一删除这些三角形。删除一个三角形有两种情况：

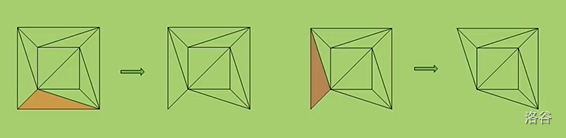
如左图情况，删除一个三角形使得 \(F\) 减一，\(E\) 减一；而右图情况，删除一个三角形使得 \(F\) 减一，\(E\) 减二，\(V\) 减一。但无论如何，\(F-E+V\) 的值依旧不变。

到了最后归纳到只有一个三角形时，\(F=1\)，\(E=3\)，\(V=3\)，那么 \(F-E+V=1\)，因为之前所做的操作都不会影响 \(F-E+V\) 的值，那么原先的平面图就有 \(F-E+V=1\)。

也就是证明了原先的凸多面体满足 \(F-E+V=2\)。

我们有一个发现，任意一个平面图是能够画在一个曲面上的。

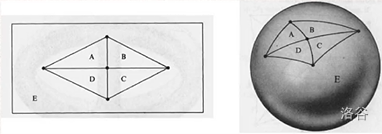
其实这相当于一个连续变换的过程，可以简单理解为把一个曲面随意拉伸扭曲使得其变形。但是不能割裂、穿孔