【1 级置顶】duel！

Z 为我胜，L 为 lnw 胜。

D 为 dcy 胜

第 1 场 Problem - 526C - Codeforces Z \(\textcolor{green}{2000}\)

看到感觉和之前某一道 ABC E 很相像，就是枚举红色吃多少个，然后计算代价，因为代价计算公式是有一个下取整的，猜测大体是单调的，但是局部内不是单调的，所以直接枚举前后两个段就可以了。然后发现 \(W_r\) 不像 AT 那道题一样很小，所以随便枚举 \([0, 10^6]\) 和 \([C/W_r-10^6,C/W_r]\) 一段。

发现跑过了非常多的点，大概50多个点才wa，觉得已经和正解很近了。查看 wa 的点，发现是：

999999999 10 499999995 2 99999999

嗯，也就是说把 \(r\) 和 \(b\) swap 一下再做一遍就可以了？

交上去就过了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll c, hr, hb, wr, wb, ans;
ll calc(ll x) {
    ll use = x * wr;
    if(use > c) return 0;
    ll less = c - use;
    ll y = less / wb;
    ans = max(ans, x * hr + y * hb);
    return x * hr + y * hb;
}
void run(ll l, ll r) {
    l = max(l, 0LL);
    r = min(r, c);
    for(ll i = l; i <= r; i++) {
        ans = max(ans, calc(i));
    }
}
int main() {
    cin >> c >> hr >> hb >> wr >> wb;
    run(0, 1000000);
    run(c / wr - 1000000, c / wr + 1);
    run(c / wb - 1000000, c / wb + 1);
    run(wr - 1000000, wr + 1000000);
    run(wb - 1000000, wb + 1000000);
    swap(hr, hb);
    swap(wr, wb);
    run(0, 1000000);
    run(c / wr - 1000000, c / wr + 1);
    run(c / wb - 1000000, c / wb + 1);
    run(wr - 1000000, wr + 1000000);
    run(wb - 1000000, wb + 1000000);
    printf("%lld\n", ans);
}

看了题解发现和 AT 那道题什么关系都没有。考虑若吃红糖 \(i\) 颗，那么吃蓝糖 \((c-iw_r)/w_b\) 颗。所以直接根号暴力即可，红糖做 \(\sqrt c\) 个，蓝糖做 \(\sqrt c\) 个，时间复杂度 \(O(\sqrt c)\)。

第 2 场 Problem - 1851F - Codeforces L \(\textcolor{orange}{1800}\)

赛时翻译软件炸掉了，把火星数的定义弄消失了，结果没看懂题……

好了不推卸责任，容易想到 01 trie，然后直接去做。

其实也可以做，但是比较麻烦。有一个简单的做法：

可以发现本题中如果两数在一位下两两不同，那么最终答案这一位下肯定为 0，否则就可以为 1，想到这里本题就很简单了，找到异或和最小的二元组即可，不过需要一点贪心处理，那就是排完序就可以线性复杂度求异或和最小的二元组了。

赛后死在异或运算优先级比比较优先级低。

#include <bits/stdc++.h>
#define N 2000010
using namespace std;
#define ll long long
ll T;
ll n, k;
struct node {
    ll idx, val;
} a[N];
void solve() {
    cin >> n >> k;
    for(int i = 1; i <= n; i ++) {
        cin >> a[i].val;
        a[i].idx = i;
    }
    sort(a + 1, a + n + 1, [](node a, node b) {
        return a.val < b.val;
    });
    // for(int i = 1; i <= n; i ++) {
    //     cerr << a[i].val << " ";
    // }
    // cerr << endl;
    ll ans = 1e18, x, y, anss;
    for(int i = 1; i < n; i ++) {
        if((a[i].val ^ a[i + 1].val) < ans) {
            ans = a[i].val ^ a[i + 1].val;
            x = a[i].idx;
            y = a[i + 1].idx;
            anss = ((1<<k) - 1) ^ (a[i].val | a[i + 1].val);
        }
    }
    cout << x << " " << y << " " << anss << endl;
}
int main() {
    cin >> T;
    while(T --) {
        solve();
    }
}

第 3 场 Problem - 1763C - Codeforces Z \(\textcolor{green}{2000}\)

lnw 没空，和 dcy 打的。

因为要上课所以看完题一个下午都没有打。

当 \(n\le 3\) 时暴力。当 \(n>3\) 时，假定最大值为 \(a_x\)，那么 \(x\) 左右一定会有一侧个数大于 \(1\) 个，让它们进行一次操作变为一样的，然后再进行一次操作变为 \(0\)，再与 \(x\) 进行一次操作变为 \(x\)。然后此时再把右边进行一次相同操作即可。也就是全部都变成了 \(a_x\)，答案就是 \(na_x\)。

#include <bits/stdc++.h>
#define N 200010
#define ll long long
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
using namespace std;
ll T, n, a[N], s[N], g[N], ans;
void dfs(ll x) {
    ll sum = 0;
    for(ll i = 1; i <= n; i++) {
        sum += a[i];
    }
    ans = max(ans, sum);
    if(x > n * 2) {
        return;
    }
    ll tmp[4];
    tmp[1] = a[1];
    tmp[2] = a[2];
    tmp[3] = a[3];
    for(ll i = 1; i <= n; i ++) {
        for(ll j = i + 1; j <= n; j ++) {
            ll temp = abs(a[i] - a[j]);
            for(ll k = i; k <= j; k ++) {
                a[k] = temp;
            }
            dfs(x + 1);
            for(ll k = i; k <= j; k ++) {
                a[k] = tmp[k];
            }
        }
    }
}
void solve() {
    cin >> n;
    s[0] = s[n + 1] = g[0] = g[n + 1] = 0;
    for(ll i = 1; i <= n; i++) {
        cin >> a[i];
        s[i] = s[i - 1] + a[i];
    }
    for(int i = n; i >= 1; i--) {
        g[i] = g[i + 1] + a[i];
    }
    ans = s[n];
    if(n == 2) ans = max(a[1] + a[2], abs(a[1] - a[2]) * 2);
    else if(n == 3) {
        dfs(1);
    }
    else {
        for(ll i = 1; i <= n; i++) {
            ans = max(ans, a[i] * n);
        }
    }
    printf("%lld\n", ans);
}
int main() {
    cin >> T;
    while(T --) {
        solve();
    }
}

第 4 场 Problem - 316E2 - Codeforces L \(\textcolor{orange}{2300}\)

第一眼可以看出是线段树，难在如何合并。

实际上只需要知道 \(f_{n+m}=f_{n-1}f_{m}+f_nf_{m+1}\) 就好了，斐波那契数列下标从 \(1\) 开始。

那么维护 \(\sum f_ia_i\) 和 \(\sum f_{i-1}a_i\) 即可，线段树操作是简单的。

#include <bits/stdc++.h>
#define P 1000000000
#define N 200010
#define ll long long
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
using namespace std;
ll n, m;
ll a[N], fib[N], sum[N], lazy[N * 4];
struct node {
    // val1: fi*ai
    // val2: fi-1*ai
    ll l, r, val1, val2;
    friend node operator+(const node &x, const node &y) {
        node res;
        res.l = x.l;
        res.r = y.r;
        res.val1 = (x.val1 + fib[x.r - x.l + 2] * y.val1 + fib[x.r - x.l + 1] * y.val2) % P;
        res.val2 = (x.val2 + fib[x.r - x.l + 1] * y.val1 + fib[x.r - x.l] * y.val2) % P;
        return res;
    }
} t[N * 4];
void build(ll l, ll r, ll pos) {
    if(l == r) {
        t[pos].val1 = a[l];
        t[pos].val2 = 0;
        t[pos].l = t[pos].r = l;
        return;
    }
    int mid = (l + r) >> 1;
    build(l, mid, ls(pos));
    build(mid + 1, r, rs(pos));
    t[pos] = t[ls(pos)] + t[rs(pos)];
}
void tag(ll l, ll r, ll pos, ll val) {
    (t[pos].val1 += val * sum[r - l + 1]) %= P;
    (t[pos].val2 += val * sum[r - l]) %= P;
    lazy[pos] += val;
}
void pushdown(ll l, ll r, ll pos) {
    ll mid = (l + r) >> 1;
    tag(l, mid, ls(pos), lazy[pos]);
    tag(mid + 1, r, rs(pos), lazy[pos]);
    lazy[pos] = 0;
}
void update(ll nl, ll nr, ll l, ll r, ll pos, ll val) {
    if(nl <= l && r <= nr) {
        tag(l, r, pos, val);
        return;
    }
    if(lazy[pos]) {
        pushdown(l, r, pos);
    }
    int mid = (l + r) >> 1;
    if(nl <= mid) {
        update(nl, nr, l, mid, ls(pos), val);
    }
    if(nr > mid) {
        update(nl, nr, mid + 1, r, rs(pos), val);
    }
    t[pos] = t[ls(pos)] + t[rs(pos)];
}
void update(ll x, ll l, ll r, ll pos, ll val) {
    if(l == r) {
        t[pos].val1 = val;
        t[pos].val2 = 0;
        return;
    }
    if(lazy[pos]) {
        pushdown(l, r, pos);
    }
    int mid = (l + r) >> 1;
    if(x <= mid) {
        update(x, l, mid, ls(pos), val);
    }
    else {
        update(x, mid + 1, r, rs(pos), val);
    }
    t[pos] = t[ls(pos)] + t[rs(pos)];
}
node query(ll nl, ll nr, ll l, ll r, ll pos) {
    if(nl <= l && r <= nr) {
        return t[pos];
    }
    if(lazy[pos]) {
        pushdown(l, r, pos);
    }
    int mid = (l + r) >> 1;
    node res;
    bool flag = 0;
    if(nl <= mid) {
        res = query(nl, nr, l, mid, ls(pos));
        flag = 1;
    }
    if(nr > mid) {
        if(flag) {
            res = res + query(nl, nr, mid + 1, r, rs(pos));
        } else {
            res = query(nl, nr, mid + 1, r, rs(pos));
        }
    }
    return res;
}
int main() {
    scanf("%lld %lld", &n, &m);
    fib[1] = fib[2] = 1;
    for(ll i = 3; i <= n; i ++) {
        fib[i] = (fib[i - 1] + fib[i - 2]) % P;
    }
    for(ll i = 1; i <= n; i ++) {
        sum[i] = (sum[i - 1] + fib[i]) % P;
    }
    for(ll i = 1; i <= n; i ++) {
        scanf("%lld", &a[i]);
    }
    build(1, n, 1);
    while(m --) {
        ll opt;
        scanf("%lld", &opt);
        if(opt == 1) {
            ll x, v;
            scanf("%lld %lld", &x, &v);
            update(x, 1, n, 1, v);
        } else if(opt == 2) {
            ll l, r;
            scanf("%lld %lld", &l, &r);
            node res = query(l, r, 1, n, 1);
            printf("%lld\n", res.val1);
        } else {
            ll l, r, v;
            scanf("%lld %lld %lld", &l, &r, &v);
            update(l, r, 1, n, 1, v);
        }
    }
}

第 5 场 Problem - B - Codeforces Z \(\textcolor{green}{2200}\)

再也不和陌生人打 duel 了。

就是给出若干个先序遍历或者后序遍历，那么它们的根的前后数的集合肯定一样，要么就完全相反。

所以可以用递归 \(solve(l,r)\) 表示处理 \([l,r]\) 的区间内的数，那么枚举这个区间的根节点 \(x\)，只需要保证 \([l,x)\) 和 \((x,r]\) 对于所有遍历的数集相同或者相反即可，可以用哈希实现。

如果数集相反，记得在递归前把它们转回来。

总共递归 \(n\) 层，每层 \(n\) 个数，枚举遍历是 \(k\) 的，那么就是 \(O(n^2k)\)。

#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
ull a[110][1000], ans[1000], b[110][1000], c[1000], d[110][1000], tmp[1000];
mt19937_64 rnd(chrono::steady_clock::now().time_since_epoch().count());
ull n, k;
void solve(ull l, ull r, ull fa) {
    if(l == r) {
        ans[a[1][l]] = fa;
        return ;
    }
    for(ull i = l; i <= r; i ++) {
        ull pos = d[1][a[1][i]];
        ull pre = b[1][pos - 1] ^ b[1][l - 1];
        ull suf = b[1][r] ^ b[1][pos];
        bool flag = 1;
        if(pre == 0 || suf == 0) flag = 0;
        // 枚举根
        for(ull j = 2; j <= k; j ++) {
            ull poss = d[j][a[1][i]];
            ull ppre = b[j][poss - 1] ^ b[j][l - 1];
            ull ssuf = b[j][r] ^ b[j][poss];
            if(ppre == pre && ssuf == suf);
            else if(ppre == suf && ssuf == pre);
            else flag = 0;
        }
        // right
        if(flag) {
            for(ull j = 2; j <= k; j ++) {
                ull poss = d[j][a[1][i]];
                ull ppre = b[j][poss - 1] ^ b[j][l - 1];
                ull ssuf = b[j][r] ^ b[j][poss];
                if(ppre == suf && ssuf == pre) {
                    ll len = 0;
                    for(ull u = poss + 1; u <= r; u ++) {
                        tmp[++ len] = a[j][u];
                    }
                    tmp[++ len] = a[j][poss];
                    for(ull u = l; u < poss; u ++) {
                        tmp[++ len] = a[j][u];
                    }
                    len = 0;
                    for(ull u = l; u <= r; u ++) {
                        a[j][u] = tmp[++ len];
                        b[j][u] = b[j][u - 1] ^ c[a[j][u]];
                        d[j][a[j][u]] = u;
                    }
                }
            }
            ans[a[1][i]] = fa;
            solve(l, pos - 1, a[1][i]);
            solve(pos + 1, r, a[1][i]);
            return;
        }
    }
}
int main() {
    scanf("%d %d", &n, &k);
    for(ull i = 1; i <= n; i ++) c[i] = rnd();
    for(ull i = 1; i <= k; i ++) {
        for(ull j = 1; j <= n; j ++) {
            scanf("%d", &a[i][j]);
            b[i][j] = b[i][j - 1] ^ c[a[i][j]];
            d[i][a[i][j]] = j;
        }
    }
    solve(1, n, -1);
    for(ull i = 1; i <= n; i ++) {
        printf("%d ", ans[i]);
    }
}

第 6 场 Problem - 785E - Codeforces Z \(\textcolor{green}{2200}\)

还是和陌生人打了一把 duel。

可以考虑分块，每个块用树状数组维护权值。然后交换两个数相当于先把它们删掉再添加，互相计算即可。

#include <bits/stdc++.h>
#define N 200010
#define ll long long
using namespace std;
int n, q, b;
ll ans;
int a[N], idx[N];
int t[500][N];
int L[500], R[500];
void upd(int t[], int x, int v) {
    for(int i = x; i <= n; i += i & -i) t[i] += v;
}
int qry(int t[], int x) {
    int res = 0;
    for(int i = x; i > 0; i -= i & -i) res += t[i];
    return res;
}
int main() {
    scanf("%d%d", &n, &q);
    b = sqrt(n * 17);
    for(int i = 1; i <= n; i ++) {
        a[i] = i;
        idx[i] = (i - 1) / b + 1;
        if(!L[idx[i]]) L[idx[i]] = i;
        R[idx[i]] = i;
    }
    for(int i = 1; i <= n; i ++) {
        upd(t[idx[i]], i, 1);
    }
    for(int i = 1; i <= q; i ++) {
        int l, r;
        scanf("%d%d", &l, &r);
        if(l == r) {
            printf("%lld\n", ans);
            continue;
        }
        if(l > r) swap(l, r);
        for(int j = 1; j < idx[l]; j ++) {
            ans -= qry(t[j], n) - qry(t[j], a[l]);
        }
        for(int j = idx[l] + 1; j <= idx[n]; j ++) {
            ans -= qry(t[j], a[l]);
        }
        for(int j = L[idx[l]]; j < l; j ++) {
            ans -= (a[j] > a[l]);
        }
        for(int j = l + 1; j <= R[idx[l]]; j ++) {
            ans -= (a[j] < a[l]);
        }
        for(int j = 1; j < idx[r]; j ++) {
            ans -= qry(t[j], n) - qry(t[j], a[r]);
        }
        for(int j = idx[r] + 1; j <= idx[n]; j ++) {
            ans -= qry(t[j], a[r]);
        }
        for(int j = L[idx[r]]; j < r; j ++) {
            ans -= (a[j] > a[r]);
        }
        for(int j = r + 1; j <= R[idx[r]]; j ++) {
            ans -= (a[j] < a[r]);
        }
        ans += (a[l] > a[r]);

        upd(t[idx[l]], a[l], -1);
        upd(t[idx[r]], a[r], -1);
        swap(a[l], a[r]);
        upd(t[idx[l]], a[l], 1);
        upd(t[idx[r]], a[r], 1);

        for(int j = 1; j < idx[l]; j ++) {
            ans += qry(t[j], n) - qry(t[j], a[l]);
        }
        for(int j = idx[l] + 1; j <= idx[n]; j ++) {
            ans += qry(t[j], a[l]);
        }
        for(int j = L[idx[l]]; j < l; j ++) {
            ans += (a[j] > a[l]);
        }
        for(int j = l + 1; j <= R[idx[l]]; j ++) {
            ans += (a[j] < a[l]);
        }
        for(int j = 1; j < idx[r]; j ++) {
            ans += qry(t[j], n) - qry(t[j], a[r]);
        }
        for(int j = idx[r] + 1; j <= idx[n]; j ++) {
            ans += qry(t[j], a[r]);
        }
        for(int j = L[idx[r]]; j < r; j ++) {
            ans += (a[j] > a[r]);
        }
        for(int j = r + 1; j <= R[idx[r]]; j ++) {
            ans += (a[j] < a[r]);
        }
        ans -= (a[l] > a[r]);

        printf("%lld\n", ans);
    }
}

第 6 场 Problem - 1765F - Codeforces 都不会 \(\textcolor{red}{2200}\)

我填 2000~2200，lnw 填 2200~2500，于是生成了一道 2200 的题。

结果感觉应该有 2700 吧。好难想。

首先考虑恰好选两个的时候 \((x_1,c_1),(x_2,c_2)\)，设两个分别取了 \((a_1,a_2)\)，希望浓度为 \(x\)，解一个方程：

\[ \begin{cases} a_1+a_2=1 \\ x_1a_1+x_2a_2=x \end{cases} \]

那么发现当 \(x=x_1\) 时 \(a_1=1,a_2=0\)，代价为 \(c_1\)，当 \(x=x_2\) 时 \(a_1=0,a_2=1\)，代价为 \(c_2\)。

其实发现代价就是连接 \((x_1,c_1)\) 和 \((x_2,c_2)\) 两个点的一个一次函数。

那么期望值就是这个这个一次函数，与 \(x=x_1\) 和 \(x=x_2\) 两条直线和 \(x\) 轴围成的梯形积起来，也就是：

\[ \dfrac{(c_1+c_2)(x_1-x_2)}{2} \]

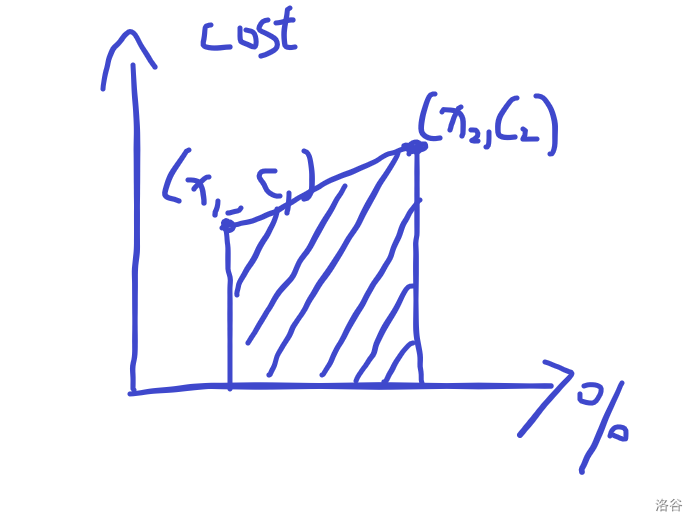
考虑更多点时，代价就是这些点围成的凸包，那么期望值也是这个凸包与两端垂直于 \(x\) 轴的直线与 \(x\) 轴围成的图形的面积了。

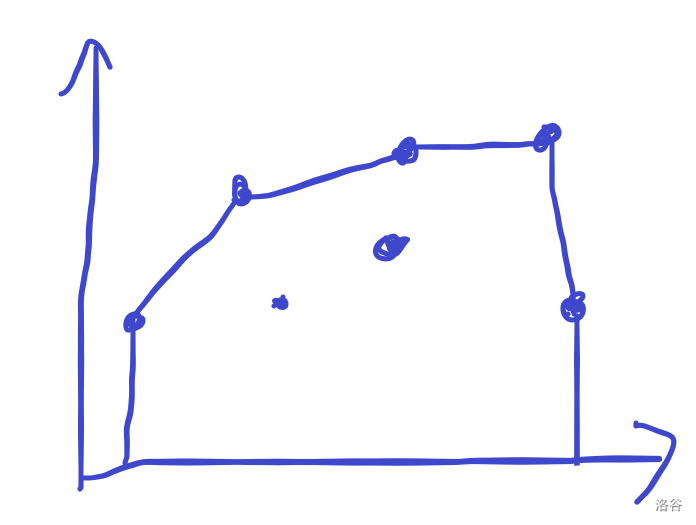
那么我们可以用 \(O(n^3)\) 维护这个凸包。考虑瓶颈是什么，就是我们要记录上一条线的斜率。但是实际上我们发现当有下面这种非凸包的情况时，一定不优（面积不比凸包大）：

所以不需要记录上一条线的斜率，dp 最优时就是凸包。

所以有：

\[ f_i=-w_i+f_j+g(j,i) \]

其中 \(g(j,i)\) 是 \(j\) 到 \(i\) 围成的面积。

时间复杂度 \(O(n^2)\)。

#include <bits/stdc++.h>
#define int long long
#define N 5010
#define db long double
using namespace std;
int n, k;
db f[N], ans;
struct node {
    int x, w, c;
} a[N];
signed main() {
    cin >> n >> k;
    for(int i = 1; i <= n; i ++) {
        cin >> a[i].x >> a[i].w >> a[i].c;
    }
    sort(a + 1, a + n + 1, [](node a, node b) {
        return a.x < b.x;
    });
    for(int i = 1; i <= n; i ++) {
        f[i] = -a[i].w;
        for(int j = 1; j < i; j ++) {
            f[i] = max(f[i], - a[i].w + f[j] + 1.0 * (a[i].x - a[j].x) * (a[i].c + a[j].c) / 200 * k);
        }
        ans = max(ans, f[i]);
    }
    cout << fixed << setprecision(10) << ans << endl;
}